PERTIDAKSAMAAN EKSPONEN DAN SIFAT-SIPATNYA
Assalamulaikum kawan, pada blog ini saya akan membahas tentang pertidaksamaan eksponen dan sifat-sifatnya. selamat belajar!
PERTIDAKSAMAAN EKSPONEN DAN SIFAT-SIPATNYA
pertidaksamaan eksponen adalah pertidaksamaan jenis eksponen yang memiliki variabel. memiliki dua ruas yaitu di ruas kanan dan ruas kiri. Bentuk umum pertidaksamaan eksponen adalah sebagai berikut. Dalam bentuk pertidaksamaan, sifat-sifat pertidaksamaan eksponen dapat diketahui sebagai berikut:


Untuk 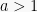
- Jika
, maka
Contoh:
Maka:
- Jika
, maka
Contoh:
Maka:
- Jika
, maka
Contoh:
Maka:
- Jika
, maka
Contoh:
Maka:
Untuk 
Jika , maka
Contoh:
Maka:
- Jika
, maka
Contoh:
Maka:
- Jika
, maka
Contoh:
Maka:
- Jika
, maka
Contoh:
Maka:

Komentar
Posting Komentar